RESISTÊNCIA DOS MATERIAIS
Um tubo é submetido a uma força de tensão de P = 9500 N. A tubulação possui diâmetro externo de 45 mm e espessura da parede de 8 mm. Sabe-se que módulo de elasticidade é E = 80 GPa. Qual a deformação especifica na tubulação expressa em mm / mm?
0,001250 mm/mm
0,005906 mm/mm
0,000982 mm/mm
0,000128 mm/mm
0,000721 mm/mm
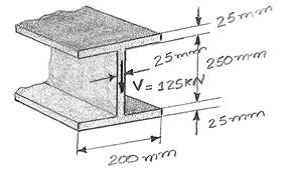
Se a viga de abas largas for submetida a um cisalhamento V = 125 kN, determine a tensão de cisalhamento máxima na viga.
Tmáx = 19,87 GPa
Tmáx = 39,87 MPa
Tmáx = 9,87 MPa
Tmáx = 29,87 MPa
Tmáx = 19,87 MPa
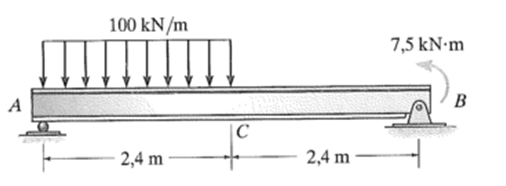
A viga simplesmente apoiada é submetida à carga mostrada na figura. Determine a deflexão em seu centro C.
δtotal = -344600/EI
δtotal = -10800/EI
δtotal = -345600/EI
δtotal = -356400/EI
δtotal = -365400/EI
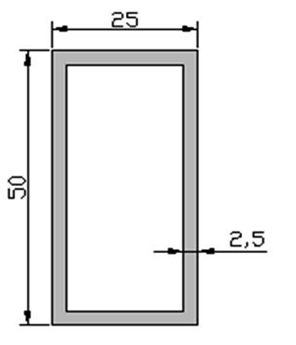
Uma barra de material de elasticidade de 160 GPa é submetida a uma força axial de tração de 100 KN. Sabe-se que a barra possui seção retangular de 25x50 mm e espessura da parede de 2,5 mm, determine a deformação específica em mm/mm.
0,000218 mm/mm
0,002356 mm/mm
0,000236 mm/mm
0,000192 mm/mm
0,001788 mm/mm
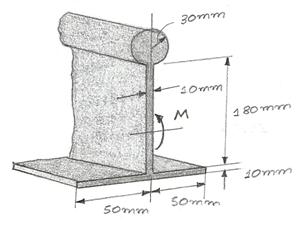
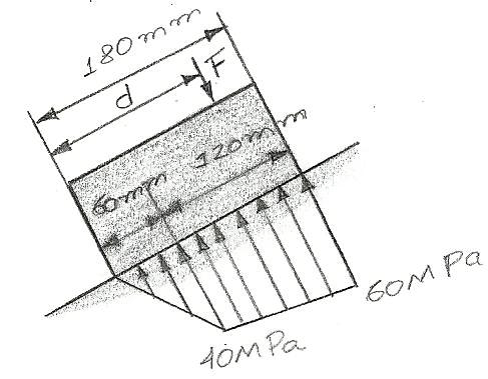
O pequeno bloco tem espessura de 5 mm. Se a distância de tensão no apoio desenvolvida pela carga variar como mostra a figura, determine a distância d até o ponto onde a força F é aplicada ao bloco.
d = 100 mm
d = 110 mm
d = 90 mm
d = 125 mm
d = 115 mm
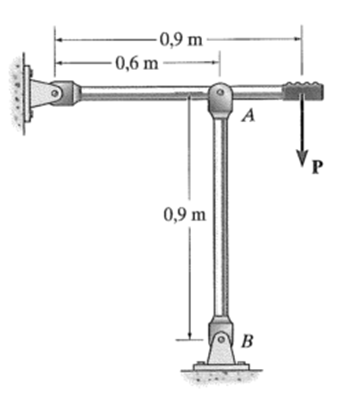
Determine a força máxima P que pode ser aplicada ao cabo, de modo que a haste de controle de aço A-36 AB não sofra flambagem. A haste tem diâmetro de 30 mm e está presa por pino nas extremidades. E = 200 GPa
P = 65.496,4 KN
P = 66.496,4 KN
P = 64.956,4 KN
P = 64.596,4 KN
P = 66.695,4 KN
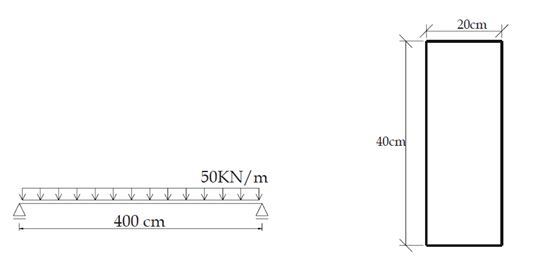
Determine a tensão normal máxima aplicada em uma viga bi-apoiada, representada abaixo, sendo que a sua seção transversal é retangular de acordo com a figura abaixo:
18,75 MPa
1,88 MPa
3,75 MPa
9,37 MPa
37,48 MPa
Uma barra de material homogêneo e isotrópico tem 500mm de comprimento e 16mm de diâmetro. Sob a ação da carga axial de 12 KN (no eixo x, coincidente com o eixo da barra), o seu comprimento aumenta de 300 μm e seu diâmetro reduz de 2,4 μm. Determinar o módulo de Elasticidade do material.
E = 99,5 GPa
E = 190 GPa
E = 105 GPa
E = 130 GPa
E = 260 GPa
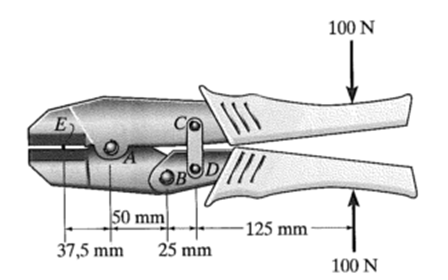
O alicate de pressão é usado para dobrar a extremidade do arame E. Se uma força de 100 N for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino em A. O pino está sujeito a cisalhamento duplo e tem diâmetro de 5 mm.
0,001250 mm/mm
0,005906 mm/mm
0,000982 mm/mm
0,000128 mm/mm
0,000721 mm/mm
Se a viga de abas largas for submetida a um cisalhamento V = 125 kN, determine a tensão de cisalhamento máxima na viga.

Tmáx = 19,87 GPa
Tmáx = 39,87 MPa
Tmáx = 9,87 MPa
Tmáx = 29,87 MPa
Tmáx = 19,87 MPa
A viga simplesmente apoiada é submetida à carga mostrada na figura. Determine a deflexão em seu centro C.

δtotal = -344600/EI
δtotal = -10800/EI
δtotal = -345600/EI
δtotal = -356400/EI
δtotal = -365400/EI
Uma barra de material de elasticidade de 160 GPa é submetida a uma força axial de tração de 100 KN. Sabe-se que a barra possui seção retangular de 25x50 mm e espessura da parede de 2,5 mm, determine a deformação específica em mm/mm.

0,000218 mm/mm
0,002356 mm/mm
0,000236 mm/mm
0,000192 mm/mm
0,001788 mm/mm
O pequeno bloco tem espessura de 5 mm. Se a distância de tensão no apoio desenvolvida pela carga variar como mostra a figura, determine a distância d até o ponto onde a força F é aplicada ao bloco.

d = 100 mm
d = 110 mm
d = 90 mm
d = 125 mm
d = 115 mm
Determine a força máxima P que pode ser aplicada ao cabo, de modo que a haste de controle de aço A-36 AB não sofra flambagem. A haste tem diâmetro de 30 mm e está presa por pino nas extremidades. E = 200 GPa

P = 65.496,4 KN
P = 66.496,4 KN
P = 64.956,4 KN
P = 64.596,4 KN
P = 66.695,4 KN
Determine a tensão normal máxima aplicada em uma viga bi-apoiada, representada abaixo, sendo que a sua seção transversal é retangular de acordo com a figura abaixo:

18,75 MPa
1,88 MPa
3,75 MPa
9,37 MPa
37,48 MPa
Uma barra de material homogêneo e isotrópico tem 500mm de comprimento e 16mm de diâmetro. Sob a ação da carga axial de 12 KN (no eixo x, coincidente com o eixo da barra), o seu comprimento aumenta de 300 μm e seu diâmetro reduz de 2,4 μm. Determinar o módulo de Elasticidade do material.
E = 99,5 GPa
E = 190 GPa
E = 105 GPa
E = 130 GPa
E = 260 GPa
O alicate de pressão é usado para dobrar a extremidade do arame E. Se uma força de 100 N for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino em A. O pino está sujeito a cisalhamento duplo e tem diâmetro de 5 mm.


Tmáx = 19,87 GPa
Tmáx = 39,87 MPa
Tmáx = 9,87 MPa
Tmáx = 29,87 MPa
Tmáx = 19,87 MPa
A viga simplesmente apoiada é submetida à carga mostrada na figura. Determine a deflexão em seu centro C.

δtotal = -344600/EI
δtotal = -10800/EI
δtotal = -345600/EI
δtotal = -356400/EI
δtotal = -365400/EI
Uma barra de material de elasticidade de 160 GPa é submetida a uma força axial de tração de 100 KN. Sabe-se que a barra possui seção retangular de 25x50 mm e espessura da parede de 2,5 mm, determine a deformação específica em mm/mm.

0,000218 mm/mm
0,002356 mm/mm
0,000236 mm/mm
0,000192 mm/mm
0,001788 mm/mm
O pequeno bloco tem espessura de 5 mm. Se a distância de tensão no apoio desenvolvida pela carga variar como mostra a figura, determine a distância d até o ponto onde a força F é aplicada ao bloco.

d = 100 mm
d = 110 mm
d = 90 mm
d = 125 mm
d = 115 mm
Determine a força máxima P que pode ser aplicada ao cabo, de modo que a haste de controle de aço A-36 AB não sofra flambagem. A haste tem diâmetro de 30 mm e está presa por pino nas extremidades. E = 200 GPa

P = 65.496,4 KN
P = 66.496,4 KN
P = 64.956,4 KN
P = 64.596,4 KN
P = 66.695,4 KN
Determine a tensão normal máxima aplicada em uma viga bi-apoiada, representada abaixo, sendo que a sua seção transversal é retangular de acordo com a figura abaixo:

18,75 MPa
1,88 MPa
3,75 MPa
9,37 MPa
37,48 MPa
Uma barra de material homogêneo e isotrópico tem 500mm de comprimento e 16mm de diâmetro. Sob a ação da carga axial de 12 KN (no eixo x, coincidente com o eixo da barra), o seu comprimento aumenta de 300 μm e seu diâmetro reduz de 2,4 μm. Determinar o módulo de Elasticidade do material.
E = 99,5 GPa
E = 190 GPa
E = 105 GPa
E = 130 GPa
E = 260 GPa
O alicate de pressão é usado para dobrar a extremidade do arame E. Se uma força de 100 N for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino em A. O pino está sujeito a cisalhamento duplo e tem diâmetro de 5 mm.


δtotal = -344600/EI
δtotal = -10800/EI
δtotal = -345600/EI
δtotal = -356400/EI
δtotal = -365400/EI
Uma barra de material de elasticidade de 160 GPa é submetida a uma força axial de tração de 100 KN. Sabe-se que a barra possui seção retangular de 25x50 mm e espessura da parede de 2,5 mm, determine a deformação específica em mm/mm.

0,000218 mm/mm
0,002356 mm/mm
0,000236 mm/mm
0,000192 mm/mm
0,001788 mm/mm
O pequeno bloco tem espessura de 5 mm. Se a distância de tensão no apoio desenvolvida pela carga variar como mostra a figura, determine a distância d até o ponto onde a força F é aplicada ao bloco.

d = 100 mm
d = 110 mm
d = 90 mm
d = 125 mm
d = 115 mm
Determine a força máxima P que pode ser aplicada ao cabo, de modo que a haste de controle de aço A-36 AB não sofra flambagem. A haste tem diâmetro de 30 mm e está presa por pino nas extremidades. E = 200 GPa

P = 65.496,4 KN
P = 66.496,4 KN
P = 64.956,4 KN
P = 64.596,4 KN
P = 66.695,4 KN
Determine a tensão normal máxima aplicada em uma viga bi-apoiada, representada abaixo, sendo que a sua seção transversal é retangular de acordo com a figura abaixo:

18,75 MPa
1,88 MPa
3,75 MPa
9,37 MPa
37,48 MPa
Uma barra de material homogêneo e isotrópico tem 500mm de comprimento e 16mm de diâmetro. Sob a ação da carga axial de 12 KN (no eixo x, coincidente com o eixo da barra), o seu comprimento aumenta de 300 μm e seu diâmetro reduz de 2,4 μm. Determinar o módulo de Elasticidade do material.
E = 99,5 GPa
E = 190 GPa
E = 105 GPa
E = 130 GPa
E = 260 GPa
O alicate de pressão é usado para dobrar a extremidade do arame E. Se uma força de 100 N for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino em A. O pino está sujeito a cisalhamento duplo e tem diâmetro de 5 mm.


0,000218 mm/mm
0,002356 mm/mm
0,000236 mm/mm
0,000192 mm/mm
0,001788 mm/mm
O pequeno bloco tem espessura de 5 mm. Se a distância de tensão no apoio desenvolvida pela carga variar como mostra a figura, determine a distância d até o ponto onde a força F é aplicada ao bloco.

d = 100 mm
d = 110 mm
d = 90 mm
d = 125 mm
d = 115 mm
Determine a força máxima P que pode ser aplicada ao cabo, de modo que a haste de controle de aço A-36 AB não sofra flambagem. A haste tem diâmetro de 30 mm e está presa por pino nas extremidades. E = 200 GPa

P = 65.496,4 KN
P = 66.496,4 KN
P = 64.956,4 KN
P = 64.596,4 KN
P = 66.695,4 KN
Determine a tensão normal máxima aplicada em uma viga bi-apoiada, representada abaixo, sendo que a sua seção transversal é retangular de acordo com a figura abaixo:

18,75 MPa
1,88 MPa
3,75 MPa
9,37 MPa
37,48 MPa
Uma barra de material homogêneo e isotrópico tem 500mm de comprimento e 16mm de diâmetro. Sob a ação da carga axial de 12 KN (no eixo x, coincidente com o eixo da barra), o seu comprimento aumenta de 300 μm e seu diâmetro reduz de 2,4 μm. Determinar o módulo de Elasticidade do material.
E = 99,5 GPa
E = 190 GPa
E = 105 GPa
E = 130 GPa
E = 260 GPa
O alicate de pressão é usado para dobrar a extremidade do arame E. Se uma força de 100 N for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino em A. O pino está sujeito a cisalhamento duplo e tem diâmetro de 5 mm.


d = 100 mm
d = 110 mm
d = 90 mm
d = 125 mm
d = 115 mm
Determine a força máxima P que pode ser aplicada ao cabo, de modo que a haste de controle de aço A-36 AB não sofra flambagem. A haste tem diâmetro de 30 mm e está presa por pino nas extremidades. E = 200 GPa

P = 65.496,4 KN
P = 66.496,4 KN
P = 64.956,4 KN
P = 64.596,4 KN
P = 66.695,4 KN
Determine a tensão normal máxima aplicada em uma viga bi-apoiada, representada abaixo, sendo que a sua seção transversal é retangular de acordo com a figura abaixo:

18,75 MPa
1,88 MPa
3,75 MPa
9,37 MPa
37,48 MPa
Uma barra de material homogêneo e isotrópico tem 500mm de comprimento e 16mm de diâmetro. Sob a ação da carga axial de 12 KN (no eixo x, coincidente com o eixo da barra), o seu comprimento aumenta de 300 μm e seu diâmetro reduz de 2,4 μm. Determinar o módulo de Elasticidade do material.
E = 99,5 GPa
E = 190 GPa
E = 105 GPa
E = 130 GPa
E = 260 GPa
O alicate de pressão é usado para dobrar a extremidade do arame E. Se uma força de 100 N for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino em A. O pino está sujeito a cisalhamento duplo e tem diâmetro de 5 mm.


P = 65.496,4 KN
P = 66.496,4 KN
P = 64.956,4 KN
P = 64.596,4 KN
P = 66.695,4 KN
Determine a tensão normal máxima aplicada em uma viga bi-apoiada, representada abaixo, sendo que a sua seção transversal é retangular de acordo com a figura abaixo:

18,75 MPa
1,88 MPa
3,75 MPa
9,37 MPa
37,48 MPa
Uma barra de material homogêneo e isotrópico tem 500mm de comprimento e 16mm de diâmetro. Sob a ação da carga axial de 12 KN (no eixo x, coincidente com o eixo da barra), o seu comprimento aumenta de 300 μm e seu diâmetro reduz de 2,4 μm. Determinar o módulo de Elasticidade do material.
E = 99,5 GPa
E = 190 GPa
E = 105 GPa
E = 130 GPa
E = 260 GPa
O alicate de pressão é usado para dobrar a extremidade do arame E. Se uma força de 100 N for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino em A. O pino está sujeito a cisalhamento duplo e tem diâmetro de 5 mm.


18,75 MPa
1,88 MPa
3,75 MPa
9,37 MPa
37,48 MPa
Uma barra de material homogêneo e isotrópico tem 500mm de comprimento e 16mm de diâmetro. Sob a ação da carga axial de 12 KN (no eixo x, coincidente com o eixo da barra), o seu comprimento aumenta de 300 μm e seu diâmetro reduz de 2,4 μm. Determinar o módulo de Elasticidade do material.
E = 99,5 GPa
E = 190 GPa
E = 105 GPa
E = 130 GPa
E = 260 GPa
O alicate de pressão é usado para dobrar a extremidade do arame E. Se uma força de 100 N for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino em A. O pino está sujeito a cisalhamento duplo e tem diâmetro de 5 mm.

E = 99,5 GPa
E = 190 GPa
E = 105 GPa
E = 130 GPa
E = 260 GPa
O alicate de pressão é usado para dobrar a extremidade do arame E. Se uma força de 100 N for aplicada nas hastes do alicate, determine a tensão de cisalhamento média no pino em A. O pino está sujeito a cisalhamento duplo e tem diâmetro de 5 mm.